Using rpact with Raw Data

Nestlé rpact Training 2024, Lausanne

Gernot Wassmer and Friedrich Pahlke

May 24, 2024

Introduction

We show how to use the function getDataset() as an utility function to process adjusted means and estimated standard deviations from raw data, how to convert the raw data into an rpact dataset, and finally how to use this information for the analysis at interim and the final stage. Essentially, this is through the use of the CRAN package emmeans that allows the extraction of least squares means from a specified model, e.g., an ANCOVA model considered here.

What will be illustrated?

  • How to import raw data from a SAS file
  • How to get the adjusted means and standard deviations from the data
  • How to convert the raw data into an dataset
  • How to analyze the dataset

Load required R packages

library(rpact)

# compute estimated marginal means (EMMs) for specified factors 
# in a linear model
library(emmeans)

Analysis of raw data – Data import from csv file

Artificial dataset that was randomly generated with simulated normal data.
The dataset has six variables:

  1. Subject id
  2. Stage number
  3. Group name
  4. An example outcome in that we are interested in
  5. The first covariate gender
  6. The second covariate covariate

data <- read.csv(file = "../files/data_two_arm_adjusted_means.csv")
data <- data[, !(colnames(data) %in% c("visit", "seed"))]
data1 <- data[data$stage == 1, ]
data2 <- data[data$stage == 2, ]
data3 <- data[data$stage == 3, ]
head(data1)
  subject stage           group   outcome gender covariate
1    1101     1 Treatment group  60.91533      m  41.74395
2    1102     1 Treatment group  57.65198      f  43.94315
3    1103     1 Treatment group 118.36755      f  38.82385
4    1104     1 Treatment group 118.25124      m  36.79198
5    1105     1 Treatment group 174.35321      f  42.92030
6    1106     1 Treatment group 113.80682      f  36.30031

Analysis of raw data – Descriptive Statistics

s1 <-aggregate(x = data$outcome, by = list(data$group,
    data$stage), FUN = mean, na.rm = TRUE)
s2 <-aggregate(x = data$outcome, by = list(data$group,
    data$stage), FUN = sd, na.rm = TRUE)
s3 <-aggregate(x = data$outcome, by = list(data$group,
    data$stage), FUN = length)
tab <- data.frame(stage = s1$Group.2,
                    arm = s1$Group.1,
                    n = s3$x,
                    mean = s1$x,
                    std = s2$x) |> 
    print()
  stage             arm  n      mean      std
1     1   Control group 87  91.66591 49.13310
2     1 Treatment group 87 110.88731 45.65258
3     2   Control group 87 101.83443 41.97826
4     2 Treatment group 87 114.06969 49.06744
5     3   Control group 87 103.31525 37.87368
6     3 Treatment group 87 112.17591 39.91061

The mean of outcome is larger in the treatment group as in the control group.

Check whether group is a character vector or factor:

class(data1$group)
[1] "character"
unique(data1$group)
[1] "Treatment group" "Control group"

Convert group to a factor (so that the order can be changed later):

data1$group <- as.factor(data1$group)

\(\hspace{1.5cm}\)

Since its first release, R has by default converted character strings to factors when creating data frames directly with data.frame() or as the result of using read.table() variants (e.g., read.csv()) to read in tabular data, i.e., stringsAsFactors = TRUE by default.

With the release of R 4.0.0 the default was changed to stringsAsFactors = FALSE!

Explore covariates

Frequency of gender levels per group:

tapply(data1$gender, data1$group, table)
$`Control group`

 f  m 
45 42 

$`Treatment group`

 f  m 
40 47

The frequency of gender has a good balance, overall and per group.

Mean of covariate per group:

tapply(data1$covariate, data1$group, mean, na.rm = TRUE)
  Control group Treatment group 
       49.96940        40.43999

The mean of covariate is larger in the control group than in the treatment group.

Interim analyses

First look: analysis at stage 1

For illustration we create a group sequential design with default parameters:

design <- getDesignGroupSequential()

Then we create a linear model with dependent variable y = outcome, independent variable group, and covariates covariate and gender, i.e., the model formula is outcome ~ group + covariate + gender:

lmResult1 <- lm(outcome ~ group + covariate + gender, data = data1)
lmResult1

Call:
lm(formula = outcome ~ group + covariate + gender, data = data1)

Coefficients:
         (Intercept)  groupTreatment group             covariate               genderm  
            139.2393               11.8357               -0.8502              -10.5387

Here we are not interested in the model output but we need it to compute the estimated marginal means (EMMs; least-squares means) for the factor group in the model:

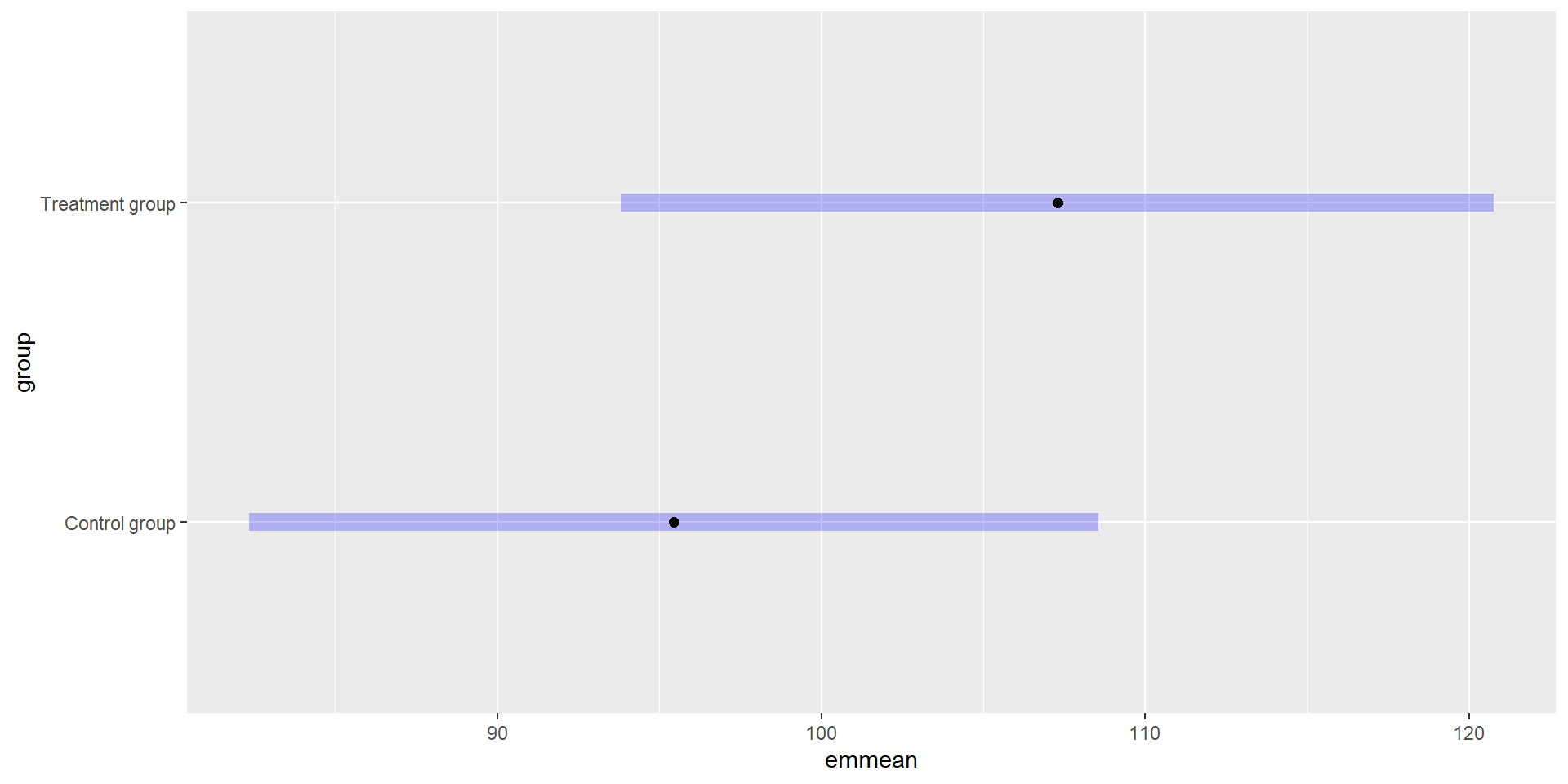
emResult1 <- emmeans(lmResult1, "group")
emResult1
 group           emmean   SE  df lower.CL upper.CL
 Control group     95.4 6.64 167     82.3      109
 Treatment group  107.3 6.82 167     93.8      121

Results are averaged over the levels of: gender 
Confidence level used: 0.95

Note that the estimated standard deviation is also included in the object.

The rpact function getDataset() directly accepts the result objects of emmeans(). To create the dataset for the first interim analysis we only have to put the object emResult1 as exclusive argument to the function getDataset():

dataset1 <- getDataset(emResult1)
dataset1

Dataset of means

  • Stages: 1, 1
  • Treatment groups: 1, 2
  • Sample sizes: 84, 87
  • Means: 107.28, 95.45
  • Standard deviations: 62.48, 61.92

Calculated data

  • Cumulative sample sizes: 84, 87
  • Cumulative means: 107.28, 95.45
  • Cumulative standard deviations: 62.48, 61.92

Check the getDataset result

The order of the group levels is important to get the correct analysis results. Therefore we do some check before we continue.

rpact expects the following group level order:

  • 1 = Treatment group
  • 2 = Control group

Carefully check and define the order of the group levels. Depending on the group names it is important to guarantee that the order is defined as expected from rpact (see above).

For correct modelling, the control group should be the reference level and is therefore set to position 1:

data1$group <- relevel(data1$group, ref = "Control group")
levels(data1$group)
[1] "Control group"   "Treatment group"

Alternative command to reorder the group levels:

data1$group <- factor(data1$group, 
                      levels = c("Control group", "Treatment group"))

If the treatment group shall be the reference level you can later add the argument directionUpper = FALSE to getAnalysisResult().

After modifying the order double check that the dataset is still correct. We do that by creating the unadjusted dataset using a simple model without covariates:

datasetCheck1 <- getDataset(
    emmeans(lm(outcome ~ group, data = data1), "group"))
tapply(datasetCheck1$means, datasetCheck1$groups, mean, na.rm = TRUE)
        1         2 
110.88731  91.66591 
tapply(data1$outcome, data1$group, mean, na.rm = TRUE)
  Control group Treatment group 
       91.66591       110.88731

The control group has a mean of 91.7 in the raw data and in the dataset, where 2 = control.

Recalculate the estimated marginal means for the complete model:

lmresult1 <- lm(outcome ~ group + covariate + gender, data = data1)
emResult1 <- emmeans(lmResult1, "group")
plot(emResult1)

The estimated marginal means and corresponding confidence intervals within the strata of the factors of the model can be obtained as follows:

emmeans(lmResult1, ~ group + covariate + gender)
 group           covariate gender emmean   SE  df lower.CL upper.CL
 Control group        45.3 f       100.7 7.45 167     86.0      115
 Treatment group      45.3 f       112.6 7.94 167     96.9      128
 Control group        45.3 m        90.2 7.68 167     75.0      105
 Treatment group      45.3 m       102.0 7.50 167     87.2      117

Confidence level used: 0.95

Analysis results of stage 1

As from above, let dataset1 be the dataset for the complete model:

analysisResults1 <- getAnalysisResults(design = design,
        dataInput = dataset1)
summary(analysisResults1)

Analysis results of stage 1

Analysis results for a continuous endpoint

Sequential analysis with 3 looks (group sequential design). The results were calculated using a two-sample t-test (one-sided, alpha = 0.025), equal variances option. H0: mu(1) - mu(2) = 0 against H1: mu(1) - mu(2) > 0.

Stage 1 2 3
Planned information rate 0.333 0.667 1
Efficacy boundary (z-value scale) 3.471 2.454 2.004
Cumulative alpha spent 0.0003 0.0072 0.0250
Stage level 0.0003 0.0071 0.0225
Cumulative effect size 11.836
Cumulative (pooled) standard deviation 62.192
Overall test statistic 1.244
Overall p-value 0.1076
Test action continue
Conditional rejection probability 0.0621
95% repeated confidence interval [-21.835; 45.506]
Repeated p-value 0.3127

The test decision at stage 1 is to not reject the null hypothesis and to continue the trial.

If the treatment group shall be the reference level you may add directionUpper = FALSE (default is TRUE):

data1b <- data1
data1b$group <- relevel(data1b$group, ref = "Treatment group")
dataset1b <- getDataset(emmeans(lm(
    outcome ~ group + covariate + gender,
    data = data1b), "group"))
analysisResults1b <- getAnalysisResults(
    design = design,
    dataInput = dataset1b, directionUpper = FALSE
)
summary(analysisResults1b)

Analysis results for a continuous endpoint

Sequential analysis with 3 looks (group sequential design). The results were calculated using a two-sample t-test (one-sided, alpha = 0.025), equal variances option. H0: mu(1) - mu(2) = 0 against H1: mu(1) - mu(2) < 0.

Stage 1 2 3
Planned information rate 0.333 0.667 1
Efficacy boundary (z-value scale) 3.471 2.454 2.004
Cumulative alpha spent 0.0003 0.0072 0.0250
Stage level 0.0003 0.0071 0.0225
Cumulative effect size -11.836
Cumulative (pooled) standard deviation 62.192
Overall test statistic -1.244
Overall p-value 0.1076
Test action continue
Conditional rejection probability 0.0621
95% repeated confidence interval [-45.506; 21.835]
Repeated p-value 0.3127

Repeated confidence interval: values turn around from [-21.8; 45.5] to [-45.5; 21.8].

Second look: analysis at stage 2

Similar to stage 1, we create a linear model with dependent variable y = outcome, independent variable group, and covariates covariate and gender:

lmResult2 <- lm(outcome ~ group + covariate + gender, data = data2)

Then we calculate the estimated marginal means of this linear model:

emResult2 <- emmeans(lmResult2, "group")

To create the dataset for the second interim analysis we only have to put the objects emResult1 and emResult2 as exclusive comma-separated arguments to the function getDataset():

dataset2 <- getDataset(emResult1, emResult2)
summary(dataset2)

Dataset of means

The dataset contains the sample sizes, means, and standard deviations of one treatment and one control group. The total number of looks is two; stage-wise and cumulative data are included.

Stage 1 1 2 2
Group 1 2 1 2
Stage-wise sample size 84 87 79 82
Cumulative sample size 84 87 163 169
Stage-wise mean 107.284 95.448 110.150 105.487
Cumulative mean 107.284 95.448 108.673 100.319
Stage-wise standard deviation 62.477 61.916 62.075 61.662
Cumulative standard deviation 62.477 61.916 62.107 61.814

Display the analysis results for stage 2:

analysisResults2 <- getAnalysisResults(design = design, dataInput = dataset2)
summary(analysisResults2)

Analysis results for a continuous endpoint

Sequential analysis with 3 looks (group sequential design). The results were calculated using a two-sample t-test (one-sided, alpha = 0.025), equal variances option. H0: mu(1) - mu(2) = 0 against H1: mu(1) - mu(2) > 0.

Stage 1 2 3
Planned information rate 0.333 0.667 1
Efficacy boundary (z-value scale) 3.471 2.454 2.004
Cumulative alpha spent 0.0003 0.0072 0.0250
Stage level 0.0003 0.0071 0.0225
Cumulative effect size 11.836 8.354
Cumulative (pooled) standard deviation 62.192 61.958
Overall test statistic 1.244 1.228
Overall p-value 0.1076 0.1101
Test action continue continue
Conditional rejection probability 0.0621 0.0412
95% repeated confidence interval [-21.835; 45.506] [-8.430 ; 25.138]
Repeated p-value 0.3127 0.2002

The test decision at stage 2 is to not reject the null hypothesis and to continue the trial.

Last look: analysis at stage 3

After collection of the additional trial data planned for stage 3, we can read the raw data, e.g., from a local csv file:

data3 <- data[data$stage == 3, ]
data3$group <- as.factor(data3$group)
data3$group <- relevel(data3$group, ref = "Control group")
head(data3)
    subject stage           group   outcome gender covariate
349    3101     3 Treatment group        NA      f  37.05855
350    3102     3 Treatment group 132.68682      m  35.38209
351    3103     3 Treatment group 116.46593      m  40.54073
352    3104     3 Treatment group  66.91700      f  40.46552
353    3105     3 Treatment group  47.36712      f  30.74220
354    3106     3 Treatment group  58.37924      f  37.44284
dim(data3)
[1] 174   6

Similar to stages 1 and 2, we create a linear model with dependent variable y = outcome, independent variabe group, and covariates covariate and gender:

lmResult3 <- lm(outcome ~ group + covariate + gender, data = data3)

Calculate the estimated marginal means of this linear model:

emResult3 <- emmeans(lmResult3, "group")

To create the dataset for the third interim analysis we only have to put the objects emResult1, emResult2, and emResult3 as exclusive comma-separated arguments to the function getDataset():

dataset3 <- getDataset(emResult1, emResult2, emResult3) 
summary(dataset3)

Dataset of means

The dataset contains the sample sizes, means, and standard deviations of one treatment and one control group. The total number of looks is three; stage-wise and cumulative data are included.

Stage 1 1 2 2 3 3
Group 1 2 1 2 1 2
Stage-wise sample size 84 87 79 82 81 84
Cumulative sample size 84 87 163 169 244 253
Stage-wise mean 107.284 95.448 110.150 105.487 113.769 101.753
Cumulative mean 107.284 95.448 108.673 100.319 110.365 100.795
Stage-wise standard deviation 62.477 61.916 62.075 61.662 53.135 52.656
Cumulative standard deviation 62.477 61.916 62.107 61.814 59.218 58.830

As final step of stage 3 we create and display the analysis results:

analysisResults3 <- getAnalysisResults(design = design, dataInput = dataset3)
summary(analysisResults3)

Analysis results for a continuous endpoint

Sequential analysis with 3 looks (group sequential design). The results were calculated using a two-sample t-test (one-sided, alpha = 0.025), equal variances option. H0: mu(1) - mu(2) = 0 against H1: mu(1) - mu(2) > 0.

Stage 1 2 3
Planned information rate 0.333 0.667 1
Efficacy boundary (z-value scale) 3.471 2.454 2.004
Cumulative alpha spent 0.0003 0.0072 0.0250
Stage level 0.0003 0.0071 0.0225
Cumulative effect size 11.836 8.354 9.570
Cumulative (pooled) standard deviation 62.192 61.958 59.021
Overall test statistic 1.244 1.228 1.807
Overall p-value 0.1076 0.1101 0.0357
Test action continue continue accept
Conditional rejection probability 0.0621 0.0412
95% repeated confidence interval [-21.835; 45.506] [-8.430 ; 25.138] [-1.070 ; 20.210]
Repeated p-value 0.3127 0.2002 0.0404
Final p-value 0.0374
Final confidence interval [-0.949; 19.884]
Median unbiased estimate 9.483

The test decision at stage 3 is reject the null hypothesis.

Multi-stage raw data import

Let us assume that the data of the different stages are not stored in different data files but in one dataset where a stage column acts as an identifier for the data of the different stages.

Question: what is an efficient way to put the data to getDataset()?

Solution

First, to enable the later usage of sapply, we write a short function that returns the emmeans of a linear model result that uses only the data at the specified stage.

fun <- function(stage, f, formula, data, specs = "group") {
    emmeans(f(formula = formula, data = data[data$stage == stage, ]), 
    specs)
}

The arguments of the function are

  • stage An integer specifying the stage number.
  • f The function which shall produce the linear model result, e.g., stats::lm.
  • formula The model formula.
  • data The data.frame containing the multi-stage raw data (must contain the column stage).
  • specs The specs argument of the emmeans() function (used to specify the name of the group column).

Read the data of all stages:

data <- read.csv(file = "../files/dataAllStages.csv")
data$group <- as.factor(data$group)

Then we use the function unique to identify the available stages in the data.frame:

stages <- sort(as.integer(unique(data$stage)))

as.integer ensures that the stages will be valid also if data$stage is a factor.

Now we can create the rpact datasets for different model formulas in one step.

Example 1: Simple model without any covariates

dataset3a <- getDataset(sapply(
    stages, fun, stats::lm, 
    outcome ~ group, data))
summary(dataset3a)

Example 1: Simple model without any covariates

Dataset of means

The dataset contains the sample sizes, means, and standard deviations of one treatment and one control group. The total number of looks is three; stage-wise and cumulative data are included.

Stage 1 1 2 2 3 3
Group 1 2 1 2 1 2
Stage-wise sample size 84 87 79 82 81 84
Cumulative sample size 84 87 163 169 244 253
Stage-wise mean 110.887 91.666 114.070 101.834 112.176 103.315
Cumulative mean 110.887 91.666 112.430 96.600 112.345 98.829
Stage-wise standard deviation 48.078 48.078 46.171 46.171 39.386 39.386
Cumulative standard deviation 48.078 48.078 47.045 47.298 44.567 44.859

Example 2: Linear model with covariates

dataset3b <- getDataset(sapply(
    stages, fun, stats::lm,
    outcome ~ group + covariate + gender, data))
summary(dataset3b)

Example 2: Linear model with covariates

Dataset of means

The dataset contains the sample sizes, means, and standard deviations of one treatment and one control group. The total number of looks is three; stage-wise and cumulative data are included.

Stage 1 1 2 2 3 3
Group 1 2 1 2 1 2
Stage-wise sample size 84 87 79 82 81 84
Cumulative sample size 84 87 163 169 244 253
Stage-wise mean 107.284 95.448 110.150 105.487 113.769 101.753
Cumulative mean 107.284 95.448 108.673 100.319 110.365 100.795
Stage-wise standard deviation 63.292 62.723 62.854 62.437 53.813 53.328
Cumulative standard deviation 63.292 62.723 62.902 62.601 59.974 59.579

Note that the simple model outcome ~ group in this example results in an analysis result that rejects the null hypothesis already at stage 2 because covariate has an effect on the outcome.

getAnalysisResults(design = design, dataInput = dataset3a) |> 
    summary()

Analysis results for a continuous endpoint

Sequential analysis with 3 looks (group sequential design). The results were calculated using a two-sample t-test (one-sided, alpha = 0.025), equal variances option. H0: mu(1) - mu(2) = 0 against H1: mu(1) - mu(2) > 0.

Stage 1 2 3
Planned information rate 0.333 0.667 1
Efficacy boundary (z-value scale) 3.471 2.454 2.004
Cumulative alpha spent 0.0003 0.0072 0.0250
Stage level 0.0003 0.0071 0.0225
Cumulative effect size 19.221 15.830 13.516
Cumulative (pooled) standard deviation 48.078 47.174 44.716
Overall test statistic 2.614 3.057 3.369
Overall p-value 0.0049 0.0012 0.0004
Test action continue reject and stop reject
Conditional rejection probability 0.3238 0.7934
95% repeated confidence interval [-6.808; 45.251] [3.051 ; 28.609] [5.455 ; 21.577]
Repeated p-value 0.0798 0.0071 0.0004
Final p-value 0.0014
Final confidence interval [5.438; 25.824]
Median unbiased estimate 15.652

Conclusions

  • getDataset supports emmeans result objects since rpact version 3.1.1
  • Easy to use: just add one emmeans result object per stage as argument of getDataset
  • rpact will support all models that are supported by emmeans, e.g., complex longitudinal models with random intercept and random slope (not yet supported)
  • Multi-arm analysis is also supported (carefully define order of treatments and control!)